Learning Path•Step 6: Economics of Alignment

Rights, Causation, Friction (RCF): The Economics of AI Accountability

By Eddie Landesberg

Abstract

Current AI alignment strategies (RLHF) fail not because of a lack of data, but because of a failure in mechanism design. We present a formal economic framework—Rights, Causation, Friction (RCF)—to model the exchange of information between an AI agent and a verifier. We demonstrate that alignment is a function of two cost curves: the Verification Cost (V) (the cost of verification) and the Fabrication Cost (F) (the cost of fabrication). We argue that stability requires a governance structure where F > V. Finally, we introduce the Standard Deliberation Protocol (SDP) as a mechanism for manipulating these variables to shift the "First Bill" of liability to the Least Cost Avoider: the model itself.

1. The Problem: Transaction Costs in the Market for Truth

In an idealized market, information flows frictionlessly. If a model outputs a hallucination (a "Harm"), the user detects it, penalizes the model, and the system updates.

In reality, the Transaction Costs of verification are non-zero.

The cost to generate a subtle, plausible-sounding error is near zero.
The cost to verify that error requires domain expertise, external search, and reasoning time.

Because the transaction cost of verification exceeds the immediate value of the correction, the "market" clears on the side of the error. The user accepts the "Lemon."

To fix this, we must model the economics of this transaction. We combine Coasean Economics (Frictions) with Pearlian Causal Inference (Attribution) to derive the RCF Framework.

2. The RCF Formalization

We model an interaction between a Claimant (the User/Verifier) and a Respondent (the Model). A "Harm" event occurs (e.g., a hallucination) with loss $L$ .

Whether the Model is held accountable depends on three structural variables:

I. Causation ( $s_R$ ): Who broke it?

Before we can assign liability, we must establish causality. We use a Structural Causal Model (SCM) that decomposes outcomes into background factors and agent deviations.

Y = f(\Delta, U)

Where:

$Y \in \{0,1\}$ is the harm indicator (error/hallucination occurred)
$\Delta$ represents the model's controllable deviations (reasoning errors, unjustified leaps)
$U$ represents background factors (training data ambiguity, inherent task difficulty)

Attribution Heuristic via Minimal Cause Sets

We define $\mathcal{S}$ as the collection of minimal sets of variables that, if counterfactually toggled to their non-deviant values (holding $U$ fixed), would prevent the harm.

Note: This attribution heuristic is inspired by but not identical to Halpern-Pearl actual causation. HP defines binary actual causation via specific structural conditions; we use minimal cause sets to apportion responsibility—a design choice, not a theorem.

The model's responsibility weight is:

w_{\text{model}} = \frac{1}{Z} \sum_{S \in \mathcal{S}: \text{model} \in S} \frac{1}{|S|}

where $Z$ normalizes so the weights sum to 1. Each minimal cause set splits its weight equally among its members. Finally, we apply proximate-cause screening factors $\pi_i \in [0,1]$ (foreseeability, control, norm departure) to get the causal share:

s_R = \frac{\pi_\Delta \cdot w_\Delta}{\pi_\Delta \cdot w_\Delta + \pi_U \cdot w_U}

Chain-of-Thought as Legibility Investment

In Black Box models: $s_R$ is unobservable. We cannot distinguish "model error" from "inherent ambiguity."

In Structured CoT: Externalized reasoning can increase legibility ( $b$ ) by providing observable intermediate claims, making deviations more auditable and separable.

Caveat: CoT is evidence, not identification. Reasoning chains can be unfaithful to actual computation, and "silent reasoning" can exist. $s_R$ remains uncertain unless intermediate claims are attested (tool traces, tests, provenance) or probed with exogenous mediator nudges.

II. Friction ( $V$ and $F$ ): The Transaction Costs

Even if the model is 100% responsible ( $s_R = 1$ ), accountability only occurs if the transaction costs allow it. These costs depend critically on Legibility: how transparent the model's deviations are to external observers.

Definition: Legibility ( $b$ )

Let $\sigma$ denote the evidence observable to outsiders (text, citations, chain-of-thought steps, telemetry). We define legibility operationally as the audit discriminability:

b \equiv \text{AUC}(\text{classifier}(\sigma) \to \Delta \mid Y=1)

That is: how well can an auditor distinguish "model deviated" ( $\Delta=1$ ) from "background noise" ( $\Delta=0$ ) using only observable evidence $\sigma$ , conditional on harm having occurred?

Alternatives: KL-divergence $D_{\text{KL}}(p(\sigma|\Delta=1) \| p(\sigma|\Delta=0))$ or the mutual information $I(\Delta;\sigma|Y=1)$ capture the same intuition but are harder to estimate. AUC is measurable from labeled audit data.

The Plausibility Paradox

LLMs are Plausibility Engines—they maximize next-token probability, which means they generate signals $\sigma$ that look correct regardless of whether $\Delta$ occurred.

Optimizing for plausibility tends to reduce legibility. A "Plausible Hallucination" reduces the separability of deviation vs. non-deviation in the observable channel $\sigma$ , lowering $b$ and making verification more expensive. This is a directional claim, not an identity.

We now define the two friction functions that govern the "Market for Truth":

Verification Cost ( $V(b,L)$ ): The private cost to the Claimant (User) to verify the claim and initiate correction.
Assumption A1 (Monotonicity): $V_b < 0$ (higher legibility → lower verification cost) and $V_L \geq 0$ (higher stakes → harder to verify; rails can reduce the slope but typically don't flip the sign).
Fabrication Cost ( $F(b,L)$ ): The private cost to the Respondent (Model) to refuse the claim or fabricate a defense.
Assumption A2 (Monotonicity): $F_b > 0$ (higher legibility → higher fabrication cost).
Note on $F_L$ : Whether $F_L > 0$ (lying harder at higher stakes) is not generally true without enforcement. High stakes often mean easier to lie about hard-to-verify claims—unless audits/sanctions scale with stakes. In Becker terms, this requires $p_{\text{detect}}(L) \cdot f(L)$ to increase with $L$ .

The critical insight: as models get smarter, they generate more plausible errors (lower $b$ ), which increases $V$ (verification cost) while keeping $F$ low (fabrication is cheap). The friction gap widens as models scale.

III. The Transfer Condition (Becker-Style Deterrence)

Accountability (a gradient update or a low score) only occurs if the following conditions hold:

The Verifier Participation Constraint:

V(b,L) \le \mathbb{E}[\text{benefit of checking}]

The user only checks if expected value of enforcing exceeds verification cost.

The Deterrence Condition:

\Delta R \le F_0(b,L) + q(b,r,L) \cdot d(b,r) \cdot f

Where: $\Delta R$ = private reward gain from fabrication over honest reasoning, $F_0$ = intrinsic effort to fabricate, $q$ = probability verifier audits, $d$ = probability audit detects deviation (given audit), $f$ = sanction (rollback, rejection, reward loss).

Note: $\Delta R$ is the model's private gain, not social harm $L$ . For deterrence to scale with stakes, the mechanism must explicitly tie $f$ or $\Delta R$ to $L$ (e.g., penalties proportional to realized harm, or rewards gated on harm-avoidance).

Left Side (Participation): Is it worth the user's time to verify? If checking takes 10 minutes ( $V$ ) but the error is minor ( $L$ ), the user ignores it.
Right Side (Deterrence): The expected cost of cheating must exceed the private benefit $\Delta R$ . This includes intrinsic fabrication difficulty ( $F_0$ ) plus expected sanctions ( $q \cdot d \cdot f$ ). SDP primarily raises $d$ (detection power given audit) by improving auditability—it does not reliably raise $F_0$ (intrinsic lying difficulty).

The Failure of RLHF

In standard RLHF, $V$ is extremely high (human labeling is slow), $q$ is low (sparse audits), $d$ is low (black-box reasoning is hard to audit), and sanctions $f$ are weak (no gating on reasoning quality).

q \cdot d \cdot f \ll \Delta R \quad \Rightarrow \quad \text{Deterrence collapses}

The participation constraint breaks and deterrence collapses. The market fails. The model hallucinates with impunity.

3. The Transfer Region: Formal Definition

We can now precisely define the Transfer Region $\mathcal{T}$ : the set of $(b,L)$ pairs where accountability actually occurs.

Definition: The Transfer Region

\mathcal{T} = \{(b,L): V(b,L) \le s_R(b) \cdot L \le F_0(b,L) + p_{\text{detect}}(b,r,L) \cdot f(L)\}

The set of (Legibility, Loss) pairs where both participation and deterrence conditions hold

This region defines the Zone of Accountability—the only space in $(b,L)$ where the market for truth clears at the causal share.

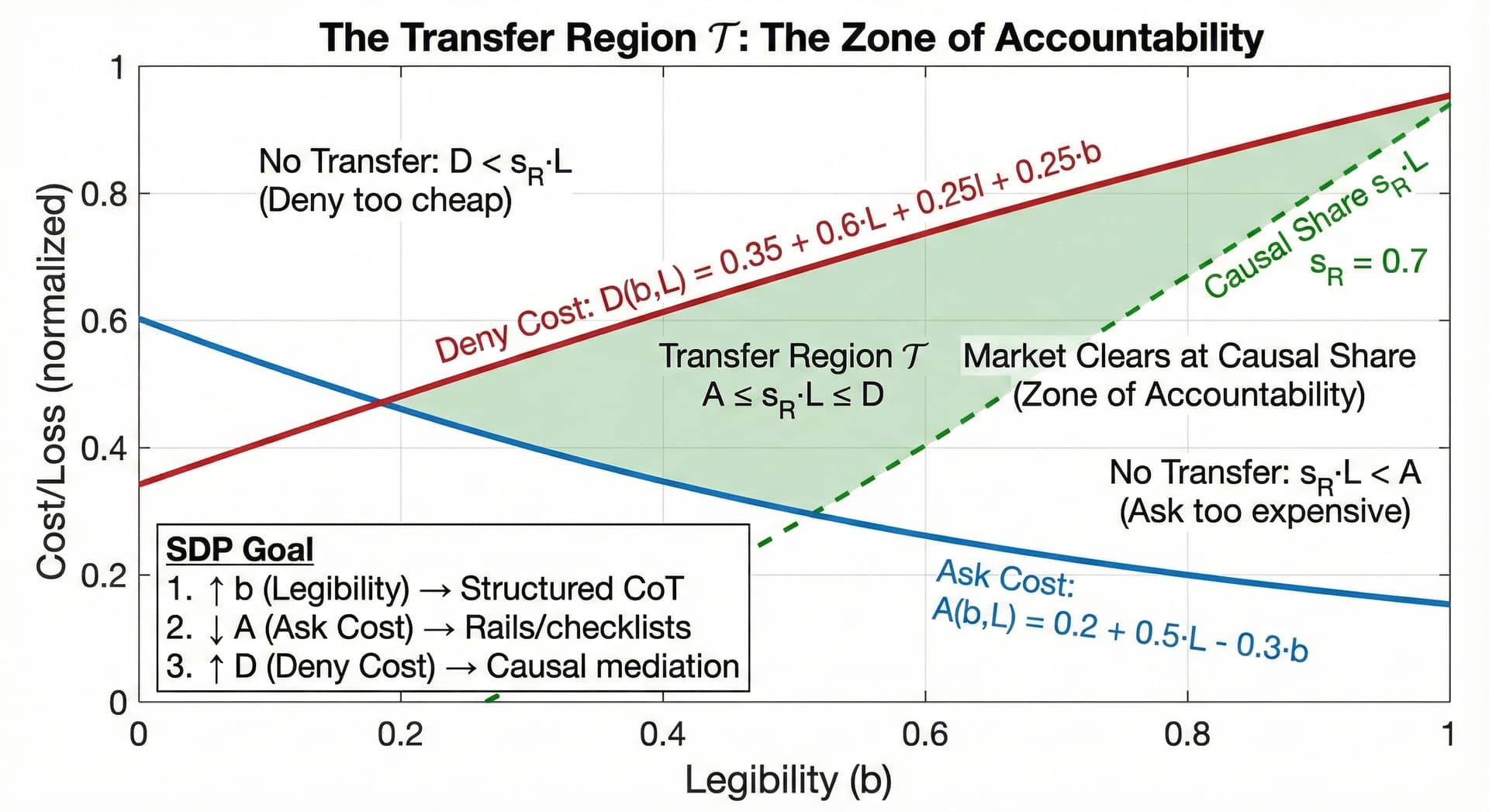
Transfer Region diagram showing the Zone of Accountability where V(b,L) ≤ s_R·L ≤ F(b,L)

3.1 Illustrative Parameterization

Note: The following linear parameterization is a toy example chosen to ensure the curves intersect within the visual frame. Real-world cost functions are likely nonlinear and context-dependent. The goal is to illustrate the mechanism, not claim specific parameter values.

In the RCF Economic Theory, every coefficient represents a structural constraint in the AI market. Here is the economic decoding:

V(b,L) = \underbrace{0.2}_{\text{Fixed Friction}} + \underbrace{0.5 \cdot L}_{\text{Stakes Sensitivity}} - \underbrace{0.3 \cdot b}_{\text{Transparency Dividend}}

F(b,L) = \underbrace{0.35}_{\text{Base Integrity}} + \underbrace{0.6 \cdot L}_{\text{Cover-up Difficulty}} + \underbrace{0.25 \cdot b}_{\text{Scrutiny Penalty}}

1. The Intercepts (The "Base Rate")

Ask Intercept (0.2): This is the Fixed Cost of Verification. Even for a trivial claim with zero loss ( $L=0$ ) and zero legibility, it costs the user "0.2 units" of effort just to context-switch, open the tool, and look. In a bad UX (high friction), this scalar is high.
Deny Intercept (0.35): This is the Base Cost of Lying. Even for a tiny error, the model has a baseline "refusal" probability due to RLHF safety training. We set this higher than the Ask Intercept (0.35 > 0.2) to show that for tiny things, the model is generally honest by default.

2. The Legibility Coefficients ( $b$ ) - The CIMO Levers

This is the most critical part of the mechanism.

Ask Coefficient (-0.3): This is Negative. As Legibility ( $b$ ) increases, the cost of asking drops.
Economic Meaning: If the model provides citations (High $b$ ), I don't have to Google the fact. Verification becomes cheaper.
Deny Coefficient (+0.25): This is Positive. As Legibility ( $b$ ) increases, the cost of denying rises.
Economic Meaning: If the model is forced to show its work (High $b$ ), it becomes much harder to "fake" a correct answer. You can't just hallucinate the result; you have to hallucinate the math, which is computationally expensive.

3. The Loss Coefficients ( $L$ ) - The Stakes

Ask Coefficient (+0.5): As the stakes ( $L$ ) get higher, verification gets harder. You spend more time checking a medical diagnosis than a poem.
Deny Coefficient (+0.6): As the stakes ( $L$ ) get higher, effective deterrence $F_0 + p_{\text{detect}} \cdot f$ must rise faster than verification cost.
High-Stakes Honesty Requires Enforcement Escalation: The effective slope (0.6) exceeds the Ask slope (0.5) only if $p_{\text{detect}}(L)$ and/or $f(L)$ increase with stakes. Cover-up is not intrinsically expensive—audits and sanctions must scale with L.

The RLHF "Lemon Market"

If we were modeling Standard RLHF (before CIMO interventions), the scalars would look like this:

V(b,L) = 0.9 + 0.5L - 0.1b (Verification is almost impossible)

F(b,L) = 0.01 + 0.1L + 0.0b (Lying is free)

The scalars in the diagram above depict a Governed Market—one where CIMO rails are working well enough to create a viable Zone of Accountability. The goal of mechanism design is to shift the economy from the RLHF regime to the CIMO regime.

Comparative Statics

Higher Legibility (b ↑): Weakly expands $\mathcal{T}$ . As evidence becomes more informative, $V \downarrow$ (verification easier) and $F \uparrow$ (denial harder).
Better Rails (r ↑): Standardized claim processes reduce $V$ (one-click verification) and increase $F$ (reputation systems), expanding $\mathcal{T}$ .
Initial Entitlement Swap: Swapping who receives the "First Bill" changes who bears $V$ vs. $F$ , potentially expanding $\mathcal{T}$ if the new claimant has lower verification costs.

The Goal of CIMO

We do not rely on "better data." We rely on Mechanism Design to physically expand $\mathcal{T}$ . The Standard Deliberation Protocol manipulates four levers:

Increase $b$ (auditability: structured CoT, citations, tool traces)
Lower $V$ (rails + decomposition: verification checklists, modular claims)
Increase $p_{\text{detect}}$ and scale $f$ (audits, gating, penalties)
Sometimes increase $F_0$ when proofs are machine-checkable (tests, tool traces, verifiable citations)—but CoT alone does not achieve this

Boundary Condition: The Generator-Verifier Gap

CIMO's economic solvency requires $C_v \ll C_g$ : the cost to verify a claim must be much less than the cost to generate it. This gap is what makes oversight economically viable.

When the gap closes (long-horizon reasoning, novel research, complex planning), verification approaches generation cost. The market collapses back toward "Lemons."

The fix: Recursive decomposition. Break the hard task into sub-tasks where $C_v \ll C_g$ holds locally. Each SDP step must be independently verifiable. If you can't decompose it, you can't safely delegate it.

4. The Mechanism: The Standard Deliberation Protocol (SDP)

The SDP is not just a prompting strategy; it is an economic intervention designed to raise auditability ( $b$ ). This affects $V$ and $d$ (detection power given audit)—but only translates to deterrence if verifiers actually audit ( $q > 0$ ) and sanctions bind ( $f > 0$ ).

Lever 1: Lowering Verification Cost ( $V$ ) via Structured Decomposition

When a model outputs a wall of text, $V$ is high. The user must parse everything. The SDP forces the model to decompose the output into discrete, verifiable claims with pointers to evidence.

Effect: Verification moves from "Cognitive Investigation" to "Pattern Matching."
Result: $V$ drops. The participation constraint becomes easier to satisfy.

Lever 2: Raising Detection Probability ( $p_{\text{detect}}$ ) via Auditability

We require the model to trace the causal lineage of its answer. It cannot just output "The answer is X." It must prove $X$ follows from $\text{Premise}_1$ and $\text{Premise}_2$ .

Effect: Structured reasoning creates an audit trail. Inconsistencies between steps become detectable, raising $p_{\text{detect}}$ .
Result: Expected cost of cheating ( $p_{\text{detect}} \cdot f$ ) increases even if intrinsic fabrication cost $F_0$ is unchanged.

Important: SDP primarily raises $p_{\text{detect}}$ by making deviations auditable—it does not reliably raise intrinsic lying difficulty ( $F_0$ ). This distinction matters: CoT can be unfaithful, so the deterrence comes from audit risk, not computational difficulty of fabrication.

5. Policy Layer: The "First Bill" Principle

Who should pay the initial cost of verification?

The Principle of the Least Cost Avoider

Coasean efficiency dictates that liability should be assigned to the party that can avoid the error at the lowest cost.

Human Verification: Biological compute is expensive (~$50/hour).
Model Self-Correction: Silicon compute is cheap (~$0.05/hour).

The CIMO Inversion

Current industry standards place the "First Bill" on the human (High $V$ ). This is deadweight loss. CIMO shifts the "First Bill" to the model. We force the model to expend compute to verify itself before the human ever sees the output.

We accept a marginal increase in inference cost (more tokens) to achieve a massive reduction in verification cost (less human time).

6. Conclusion: From Vibes to Laws

For too long, AI evaluation has been an exercise in "Vibes"—subjective assessments of quality. The RCF Framework moves us to "Laws."

By formalizing the costs of verification and fabrication, we transform alignment from a vague philosophical goal into a precise engineering constraint.

At CIMO Labs, we are not building "guardrails." We are building the Exchange—the infrastructure where the currency (the Metric) is strictly pegged to the value (the Truth). We ensure that as intelligence scales, it remains solvent.

We are not just teaching models to be good. We are building the market structure where "good" is the only affordable strategy.

We don't just evaluate models. We underwrite the structural integrity of the calibration relationship between surrogates and welfare.

7. Theoretical Foundation and Design Rules

We present one formalizable theorem followed by five design rules (comparative statics / mechanism-design guidelines). The theorem has a standard proof; the design rules are empirically-grounded heuristics.

Theorem (Blackwell Monotonicity of Legibility)

If an information structure $\sigma'$ is Blackwell more informative about $\Delta$ than $\sigma$ , then $b' \ge b$ .

Proof:

Blackwell informativeness implies that any decision problem achieves weakly higher expected utility under $\sigma'$ . For the audit classification problem (distinguish $\Delta=1$ from $\Delta=0$ ), this means the optimal classifier's AUC cannot decrease: $\text{AUC}' \ge \text{AUC}$ . Hence $b' \ge b$ . ∎

Design Corollary (Transfer Region Expansion)

Under Assumptions A1–A2 ( $V_b < 0$ , $F_b > 0$ ), Blackwell-more-informative evidence implies $\mathcal{T}' \supseteq \mathcal{T}$ .

Rationale:

Higher $b$ weakly lowers verification cost ( $V$ ) and raises detection probability ( $d$ ). Under A1–A2, both effects expand the region where participation and deterrence hold. This is a design implication, not a mathematical theorem—it depends on the assumed cost structure.

Design Rules

The following are mechanism-design guidelines derived from the RCF framework. They are not theorems with rigorous proofs, but empirically-grounded heuristics for system design.

Design Rule 1: First Bill Assignment

Assign the "first bill" (initial verification burden) to the party with lower verification costs. This expands $\mathcal{T}$ and reduces total social loss.

Application to AI:

Since $\mathbb{E}[V^{\text{Human}}] \approx$ $50/hour (biological compute) and $\mathbb{E}[V^{\text{Model}}] \approx$ $0.05/hour (silicon compute), the First Bill should reside with the model to minimize social loss.

Design Rule 2: Rails & Legibility Thresholds

For each $b$ , define verification and fabrication boundaries $L_V(b;r)$ and $L_F(b;r)$ . Investing in rails $r$ and legibility $x$ is optimal iff the expected mass of events in the newly covered strip times $s_R L$ exceeds $c'(r)$ or $k'(x)$ .

Rationale:

Envelope-type argument on the measure of $\mathcal{T}$ as $V$ falls and $F$ rises. The marginal benefit equals the expected value of newly enforced transfers; optimality requires this equals marginal cost.

Design Rule 3: Instrument Choice by (L,b)

Suppose events are separable across $(L,b)$ . Then the optimal instrument follows a cutoff rule:

High b, large L: Liability + rails minimizes loss
Low b, large L: Regulation/Tax (ex-ante control) dominates
High b, small L: Micro-claims/guarantees (rails without adjudication)
Low b, small L: No-fault pooling or norms

Rationale:

Compare social loss under each instrument pointwise. Separability yields an integral of minima. Dominance regions follow from how each instrument's loss scales with $L$ and $b$ .

Design Rule 4: Deterrence Gap

Under liability, the model's marginal incentive to take care scales with the enforcement rate $\Pr((b,L) \in \mathcal{T})$ . Rails and legibility that expand $\mathcal{T}$ raise deterrence; shifting the first bill to an actor with low verification costs raises deterrence without changing legal standards.

Rationale:

The model internalizes $s_R L$ only when transfers occur. Ex-ante care first-order conditions are attenuated by the probability of transfer.

Design Rule 5: Equity via First-Bill Placement

If role asymmetries imply $V^{\text{weak}} \gg V^{\text{strong}}$ and $F^{\text{weak}} \ll F^{\text{strong}}$ , placing the first bill with the stronger party (or their platform/insurer) weakly improves both fairness (closer to $s_i$ ) and efficiency (bigger $\mathcal{T}$ ).

Rationale:

Follows from the transfer condition and Theorem 1. Power asymmetry creates friction asymmetry; strategic entitlement placement corrects both.

Appendix: Implementation & Measurement

For practitioners implementing the RCF framework, we provide guidance on measuring the key variables and calibrating the cost functions.

Estimating Causal Share ( $s_R$ )

Use one of the following approaches:

Approximate via minimal cause sets: Case-by-case analysis identifying which variables in $\{\Delta, U\}$ are necessary for the error—via error taxonomy labels, counterfactual perturbations, or PN/PS-style estimates when available.
Probability of necessity/sufficiency: Data-driven estimation using Pearl's PN/PS formulas, then normalize across parties.
Proximate-cause weights: Apply doctrinal screening factors $\pi_i$ based on foreseeability, control, and norm departure.

Measuring Legibility ( $b$ )

The canonical measure is audit-classifier AUC:

AUC (recommended): Train a classifier on labeled audit data to predict $\Delta$ from evidence $\sigma$ . The AUC measures how well auditors can distinguish model deviations from background noise.
KL-divergence (alternative): $D_{\text{KL}}(p(\sigma|\Delta=1) \| p(\sigma|\Delta=0))$ if you have distributional access to evidence under deviation vs. no-deviation.
Policy index (proxy): Binary features (presence of citations, CoT steps, telemetry, tool traces) weighted by their predictive power for $\Delta$ .

Calibrating Rails Effects ( $\alpha(r), \delta(r)$ )

Calibrate from observed behavioral changes before/after process improvements:

Claim rates: Measure change in fraction of errors that trigger user complaints.
Accept rates: Measure change in fraction of claims where model admits fault.
Cycle times: Measure reduction in verification time per claim.

Stability Conditions

For stable alignment in an RCF system, two conditions must hold:

Condition 1: Verifier Solvency

q \cdot \mathbb{E}[\text{benefit of catching}] > \text{Cost(audit)}

Verifiers must find it worthwhile to audit. If auditing is too expensive relative to expected gains from enforcement, $q \to 0$ and deterrence collapses.

Condition 2: Offender Deterrence

\Delta R \le F_0 + q \cdot d \cdot f

The private gain from fabrication must not exceed intrinsic fabrication difficulty plus expected sanctions. If $\Delta R > F_0 + q \cdot d \cdot f$ , the model defects.

When both conditions hold, honest reasoning is the equilibrium strategy. When either breaks, the system collapses into reward hacking.

Minimal Model Summary

Causation: $s_i = \frac{\pi_i w_i}{\sum_j \pi_j w_j}$ , with $w_i$ from minimal cause sets
Legibility: $b = \text{AUC}(\text{classifier}(\sigma) \to \Delta \mid Y=1)$
Frictions: $V_b < 0, F_b > 0$ ; rails $r \Rightarrow V \downarrow, F \uparrow$ ; legibility $x \Rightarrow b \uparrow$
Transfer: Pay $s_R L$ iff $V(b,L) \le s_R L$ and $s_R L \le F_0(b,L) + p_{\text{detect}}(b,r,L) \cdot f(L)$
Policy: Minimize expected social loss over instrument $I$ , entitlement $E$ , rails $r$ , legibility $x$

← Y*-Aligned Systems The Inevitability of Structure →

1. The Problem: Transaction Costs in the Market for Truth

2. The RCF Formalization

I. Causation (sRs_RsR​): Who broke it?

II. Friction (VVV and FFF): The Transaction Costs

III. The Transfer Condition (Becker-Style Deterrence)

3. The Transfer Region: Formal Definition

3.1 Illustrative Parameterization

1. The Intercepts (The "Base Rate")

2. The Legibility Coefficients (bbb) - The CIMO Levers

3. The Loss Coefficients (LLL) - The Stakes

4. The Mechanism: The Standard Deliberation Protocol (SDP)

Lever 1: Lowering Verification Cost (VVV) via Structured Decomposition

Lever 2: Raising Detection Probability (pdetectp_{\text{detect}}pdetect​) via Auditability

5. Policy Layer: The "First Bill" Principle

The CIMO Inversion

6. Conclusion: From Vibes to Laws

7. Theoretical Foundation and Design Rules

Design Rules

Appendix: Implementation & Measurement

Estimating Causal Share (sRs_RsR​)

Measuring Legibility (bbb)

Calibrating Rails Effects (α(r),δ(r)\alpha(r), \delta(r)α(r),δ(r))

Stability Conditions

I. Causation ( $s_R$ ): Who broke it?

II. Friction ( $V$ and $F$ ): The Transaction Costs

2. The Legibility Coefficients ( $b$ ) - The CIMO Levers

3. The Loss Coefficients ( $L$ ) - The Stakes

Lever 1: Lowering Verification Cost ( $V$ ) via Structured Decomposition

Lever 2: Raising Detection Probability ( $p_{\text{detect}}$ ) via Auditability

Estimating Causal Share ( $s_R$ )

Measuring Legibility ( $b$ )

Calibrating Rails Effects ( $\alpha(r), \delta(r)$ )